Алгоритм предварительной перестановки

Теперь рассмотрим конкретную реализацию БПФ. Пусть имеется N=2^T элементов последовательности x_{N} и надо получить последовательность X_{N}. Прежде всего, нам придется разделить x_{N} на две последовательности: четные и нечетные элементы. Затем точно так же поступить с каждой последовательностью. Этот итерационный процесс закончится, когда останутся последовательности длиной по 2 элемента. Пример процесса для N=16 показан ниже:

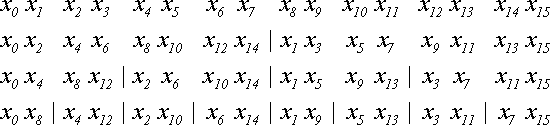
Итого выполняется (log₂N)-1 итераций.

Рассмотрим двоичное представление номеров элементов и занимаемых ими мест. Элемент с номером 0 (двоичное 0000) после всех перестановок занимает позицию 0 (0000), элемент 8 (1000) - позицию 1 (0001), элемент 4 (0100) - позицию 2 (0010), элемент 12 (1100) - позицию 3 (0011). И так далее. Нетрудно заметить связь между двоичным представлением позиции до перестановок и после всех перестановок: они зеркально симметричны. Двоичное представление конечной позиции получается из двоичного представления начальной позиции перестановкой битов в обратном порядке. И наоборот.

Этот факт не является случайностью для конкретного N=16, а является закономерностью. На первом шаге четные элементы с номером n переместились в позицию n/2, а нечетные из позиции в позицию N/2+(n-1)/2. Где n=0,1,…,N-1. Таким образом, новая позиция вычисляется из старой позиции с помощью функции:

ror(n,N) = [n/2] + N{n/2}

Здесь как обычно [x] означает целую часть числа, а {x} - дробную.

В ассемблере эта операция называется циклическим сдвигом вправо (ror), если N - это степень двойки. Название операции происходит из того факта, что берется двоичное представление числа n, затем все биты, кроме младшего (самого правого) перемещаются на 1 позицию вправо. А младший бит перемещается на освободившееся место самого старшего (самого левого) бита.

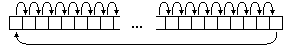
рис. 1

Дальнейшие разбиения выполняются аналогично. На каждом следующем шаге количество последовательностей удваивается, а число элементов в каждой из них уменьшается вдвое. Операции ror подвергаются уже не все биты, а только несколько младших (правых). Старшие же j-1 битов остаются нетронутыми (зафиксированными), где j - номер шага:

рис. 2

Что происходит с номерами позиций при таких последовательных операциях? Давайте проследим за произвольным битом номера позиции. Пусть этот бит находился в j-м двоичном разряде, если за 0-й разряд принять самый младший (самый правый). Бит будет последовательно сдвигаться вправо на каждом шаге до тех пор, пока не окажется в самой правой позиции. Это случится после j-го шага. На следующем, j+1-м шаге будет зафиксировано j старших битов и тот бит, за которым мы следим, переместится в разряд с номером T-j-1. После чего окажется зафиксированным и останется на месте. Но именно такое перемещение - из разряда j в разряд T-j-1 и необходимо для зеркальной перестановки бит. Что и требовалось доказать.

Теперь, мы убедились в том, что перестановка элементов действительно осуществляется по принципу, при котором в номерах позиций происходит в свою очередь другая перестановка: зеркальная перестановка двоичных разрядов. Это позволит нам получить простой алгоритм:

for(I = 1; I < N-1; I++)
{
    J = reverse(I,T);           // reverse переставляет биты в I в обратном порядке
    if (I >= J)                     // пропустить уже переставленные
        conitnue;
    S = x[I]; x[I] = x[J]; x[J] = S;  // перестановка элементов xI и xJ
}

Некоторую проблему представляет собой операция обратной перестановки бит номера позиции reverse(), которая не реализована ни в популярной архитектуре Intel, ни в наиболее распространенных языках программирования. Приходится реализовывать ее через другие битовые операции. Ниже приведен алгоритм функции перестановки T младших битов в числе I:

unsigned int reverse(unsigned int I, int T)
{
    int Shift = T - 1;
    unsigned int LowMask = 1;
    unsigned int HighMask = 1 << Shift;
    unsigned int R;
    for(R = 0; Shift >= 0; LowMask <<= 1, HighMask >>= 1, Shift -= 2)
        R |= ((I & LowMask) << Shift) | ((I & HighMask) >> Shift);
    return R;
}

Пояснения к алгоритму. В переменных LowMask и HighMask хранятся маски, выделяющие два переставляемых бита. Первая маска в двоичном представлении выглядит как 0000…001 и в цикле изменяется, сдвигая единицу каждый раз на 1 разряд влево:

0000...001
0000...010
0000...100
...

Вторая маска (HighMask) принимает последовательно значения:

1000...000
0100...000
0010...000
..., 

каждую итерацию сдвигая единичный бит на 1 разряд вправо. Эти два сдвига осуществляются инструкциями LowMask <<= 1 и HighMask >>= 1.

Переменная Shift показывает расстояние (в разрядах) между переставляемыми битами. Сначала оно равно T-1 и каждую итерацию уменьшается на 2. Цикл прекращается, когда расстояние становится меньше или равно нулю.

Операция I & LowMask выделяет первый бит, затем он сдвигается на место второго (<<Shift). Операция I & HighMask выделяет второй бит, затем он сдвигается на место первого (>>Shift). После чего оба бита записываются в переменную R операцией "|".

Вместо того чтобы переставлять биты позиций местами, можно применить и другой метод. Для этого надо вести отсчет 0,1,2,…,N/2-1 уже с обратным следованием битов. Опять-таки, ни в ассемблере Intel, ни в распространенных языках программирования не реализованы операции над обратным битовым представлением. Но алгоритм приращения на единицу известен, и его можно реализовать программно. Вот пример для T=4.

I = 0;
J = 0;
for(J1 = 0; J1 < 2; J4++, J ^= 1)
    for(J2 = 0; J2 < 2; J3++, J ^= 2)
        for(J4 = 0; J4 < 2; J4++, J ^= 4)
            for(J8 = 0; J8 < 2; J8++, J ^= 8)
            {
                if (I < J)
                {
                    S = x[I]; x[I] = x[J]; x[J] = S;  // перестановка элементов xIи xJ
                }
                I++;
            }

В этом алгоритме используется тот общеизвестный факт, что при увеличении числа от 0 до бесконечности (с приращением на единицу) каждый бит меняется с 0 на 1 и обратно с определенной периодичностью: младший бит - каждый раз, следующий - каждый второй раз, следующий - каждый четвертый и так далее.

Эта периодичность реализована в виде T вложенных циклов, в каждом из которых один из битов позиции J переключается туда и обратно с помощью операции XOR (В C/C++ она записывается как ^=). Позиция I использует обычный инкремент I++, уже встроенный в язык программирования.

Данный алгоритм имеет тот недостаток, что требует разного числа вложенных циклов в зависимости от T. На практике это не очень плохо, поскольку T обычно ограничено некоторым разумным пределом (16..20), так что можно написать столько вариантов алгоритма, сколько нужно. Тем не менее, это делает программу громоздкой. Ниже я предлагаю вариант этого алгоритма, который эмулирует вложенные циклы через стеки Index и Mask.

int Index[MAX_T];
int Mask[MAX_T];
int R;
for(I = 0; I < T; I++)
{
    Index[I] = 0;
    Mask[I] = 1 << (T - I - 1);
}
 
J = 0;
 
for(I = 0; I < N; I++)
{
    if (I < J)
    {
        S = x[I]; x[I] = x[J]; x[J] = S;  // перестановка элементов xI и xJ
    }
    for(R = 0; R < T; R++)
    {
        J ^= Mask[R];
        if (Index[R] ^= 1)  // эквивалентно Index[R] ^= 1; if (Index[R] != 0)
            break;
    }
}

Величина MAX_T определяет максимальное значение для T и в наихудшем случае равна разрядности целочисленных переменных ЭВМ. Этот алгоритм, может быть, чуть медленнее, чем предыдущий, но дает экономию по объему кода.

И, наконец, последний алгоритм. Он использует классический подход к многоразрядным битовым операциям: надо разделить 32-бита на 4 байта, выполнить перестановку в каждом из них, после чего переставить сами байты.

Перестановку бит в одном байте уже можно делать по таблице. Для нее нужно заранее приготовить массив reverse256 из 256 элементов. Этот массив будет содержать 8-битовые числа. Записываем туда числа от 0 до 255 и переставляем в каждом порядок битов.

Теперь этот массив применим для последней реализации функции reverse:

unsigned int reverse(unsigned int I, int T)
{
    unsigned int R;
    unsigned char *Ic = (unsigned char*) &I;
    unsigned char *Rc = (unsigned char*) &R;
    Rc[0] = reverse256[Ic[3]];
    Rc[1] = reverse256[Ic[2]];
    Rc[2] = reverse256[Ic[1]];
    Rc[3] = reverse256[Ic[0]];
    R >>= (32 - T);
    Return R;
}

Обращения к массиву reverse256 переставляют в обратном порядке биты в каждом байте. Указатели Ic и Ir позволяют обратиться к отдельным байтам 32-битных чисел I и R и переставить в обратном порядке байты. Сдвиг числа R вправо в конце алгоритма устраняет различия между перестановкой 32 бит и перестановкой T бит. Ниже приводится наглядная геометрическая иллюстрация алгоритма, где стрелками показаны перестановки битов, байтов и сдвиг.

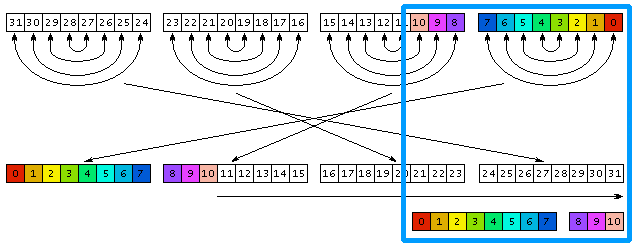
рис. 3

Оценим сложность описанных алгоритмов. Понятно, что все они пропорциональны N с каким-то коэффициентом. Точное значение коэффициента зависит от конкретной ЭВМ. Во всех случаях мы имеем N перестановок со сравнением I и J, которое предотвращает повторную перестановку некоторых элементов. Рядом присутствует некоторый обрамляющий код, применяющий достаточно быстрые операции над целыми числами: присваивания, сравнения, индексации, битовые операциии и условные переходы. Среди них в архитектуре Intel наиболее накладны переходы. Поэтому я бы рекомендовал последний алгоритм. Он содержит всего N переходов, а не 2N как в алгоритме со вложенными циклами или их эмуляцией и не NT как в самом первом алгоритме.

С другой стороны, предварительная перестановка занимает мало времени по сравнению с последующими операциями, использующими (N/2)log₂N умножений комплексных чисел. В таком случае тоже есть смысл выбрать не самый короткий, но самый простой и наглядный алгоритм - последний описанный. Вот его окончательный вид с небольшой оптимизацией:

static unsigned char reverse256[]= {
    0x00, 0x80, 0x40, 0xC0, 0x20, 0xA0, 0x60, 0xE0,
    0x10, 0x90, 0x50, 0xD0, 0x30, 0xB0, 0x70, 0xF0,
    0x08, 0x88, 0x48, 0xC8, 0x28, 0xA8, 0x68, 0xE8,
    0x18, 0x98, 0x58, 0xD8, 0x38, 0xB8, 0x78, 0xF8,
    0x04, 0x84, 0x44, 0xC4, 0x24, 0xA4, 0x64, 0xE4,
    0x14, 0x94, 0x54, 0xD4, 0x34, 0xB4, 0x74, 0xF4,
    0x0C, 0x8C, 0x4C, 0xCC, 0x2C, 0xAC, 0x6C, 0xEC,
    0x1C, 0x9C, 0x5C, 0xDC, 0x3C, 0xBC, 0x7C, 0xFC,
    0x02, 0x82, 0x42, 0xC2, 0x22, 0xA2, 0x62, 0xE2,
    0x12, 0x92, 0x52, 0xD2, 0x32, 0xB2, 0x72, 0xF2,
    0x0A, 0x8A, 0x4A, 0xCA, 0x2A, 0xAA, 0x6A, 0xEA,
    0x1A, 0x9A, 0x5A, 0xDA, 0x3A, 0xBA, 0x7A, 0xFA,
    0x06, 0x86, 0x46, 0xC6, 0x26, 0xA6, 0x66, 0xE6,
    0x16, 0x96, 0x56, 0xD6, 0x36, 0xB6, 0x76, 0xF6,
    0x0E, 0x8E, 0x4E, 0xCE, 0x2E, 0xAE, 0x6E, 0xEE,
    0x1E, 0x9E, 0x5E, 0xDE, 0x3E, 0xBE, 0x7E, 0xFE,
    0x01, 0x81, 0x41, 0xC1, 0x21, 0xA1, 0x61, 0xE1,
    0x11, 0x91, 0x51, 0xD1, 0x31, 0xB1, 0x71, 0xF1,
    0x09, 0x89, 0x49, 0xC9, 0x29, 0xA9, 0x69, 0xE9,
    0x19, 0x99, 0x59, 0xD9, 0x39, 0xB9, 0x79, 0xF9,
    0x05, 0x85, 0x45, 0xC5, 0x25, 0xA5, 0x65, 0xE5,
    0x15, 0x95, 0x55, 0xD5, 0x35, 0xB5, 0x75, 0xF5,
    0x0D, 0x8D, 0x4D, 0xCD, 0x2D, 0xAD, 0x6D, 0xED,
    0x1D, 0x9D, 0x5D, 0xDD, 0x3D, 0xBD, 0x7D, 0xFD,
    0x03, 0x83, 0x43, 0xC3, 0x23, 0xA3, 0x63, 0xE3,
    0x13, 0x93, 0x53, 0xD3, 0x33, 0xB3, 0x73, 0xF3,
    0x0B, 0x8B, 0x4B, 0xCB, 0x2B, 0xAB, 0x6B, 0xEB,
    0x1B, 0x9B, 0x5B, 0xDB, 0x3B, 0xBB, 0x7B, 0xFB,
    0x07, 0x87, 0x47, 0xC7, 0x27, 0xA7, 0x67, 0xE7,
    0x17, 0x97, 0x57, 0xD7, 0x37, 0xB7, 0x77, 0xF7,
    0x0F, 0x8F, 0x4F, 0xCF, 0x2F, 0xAF, 0x6F, 0xEF,
    0x1F, 0x9F, 0x5F, 0xDF, 0x3F, 0xBF, 0x7F, 0xFF,
};
 
 
unsigned int I, J;
unsigned char *Ic = (unsigned char*) &I;
unsigned char *Jc = (unsigned char*) &J;
 
for(I = 1; I < N - 1; I++)
{
    Jc[0] = reverse256[Ic[3]];
    Jc[1] = reverse256[Ic[2]];
    Jc[2] = reverse256[Ic[1]];
    Jc[3] = reverse256[Ic[0]];
    J >>= (32 - T);
    if (I < J)
    {
        S = x[I];
        x[I] = x[J];
        x[J] = S;
    }
}