Основной цикл алгоритма

Напомним основные формулы:

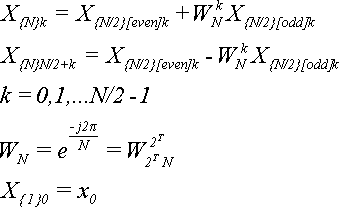(16)

На рисунке проиллюстрирован второй этап вычисления ДПФ. Линиями сверху вниз показано использование элементов для вычисления значений новых элментов. Очень удобно то, что два элемента на определенных позициях в массиве дают два элемента на тех же местах. Только принадлежать они будут уже другим, более длинным массивам, размещенным на месте прежних, более коротких. Это позволяет обойтись одним массивом данных для исходных данных, результата и хранения промежуточных результатов для всех T итераций.

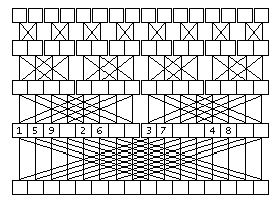
рис. 4

Итак, вот действия, которые нужно выполнить после первичной перестановки элементов.

#define T 4
#define Nmax (2 << T)
complex Q, Temp, j(0,1);
static complex x[Nmax];
static double pi2 = 2 * 3.1415926535897932384626433832795;
int N, Nd2, k, kpNd2, m;
 
for(N = 2, Nd2 = 1; N <= Nmax; Nd2 = N, N += N)
{
    for(k = 0; k < Nd2; k++)
    {
         W = exp(-j*pi2*k/N);
         for(m = k; m < Nmax; m += N)
         {
             kpNd2 = m + Nd2;
             Temp = W * x[kpNd2];
             x[kpNd2] = x[m] - Temp;
             x[m] = x[m] + Temp;
         }
    }
} 

Переменная Nmax содержит полную длину массива данных и окончательное количество элементов ДПФ. В таблице показано соответствие между выражениями в формуле (16) и переменными в программе.

В алгоритме	В формуле
N	N
Nd2	N/2
k	k
m	k с поправкой на номер последовательности
kpNd2	k+N/2 с поправкой на номер последовательности
pi2	2π
j	j (мнимая единица)
x[k] (в начале цикла)	X{N/2}[even]k
x[kpNd2] (в начале цикла)	X{N/2}[odd]k
x[k] (в конце цикла)	X{N}k
x[kpNd2] (в конце цикла)	X{N}N/2+k
W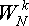

Внешний цикл - это основные итерации. На каждой из них 2Nmax/N ДПФ (длиной по N/2 элементов каждое) преобразуются в Nmax/N ДПФ  (длиной по N элементов каждое).

Следующий цикл по k представляет собой цикл синхронного вычисления элементов с индексами k и k + N/2 во всех результирующих ДПФ.

Самый внутренний цикл перебирает Nmax/N штук ДПФ одно за другим.

Именно так, а не иначе: сначала вычисляются элементы с номерами 0 и N/2, во всех ДПФ в количестве Nmax/N штук, потом с номерами 1 и N/2 + 1 и так далее. На рис.4 показана последовательность вычислений для N = 8. Такая последовательность обеспечивает однократное вычисление .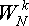

Обратите внимание, что x[kpNd2] вычисляется раньше, чем x[k], чтобы значение x[k] не было модифицировано прежде, чем будет использовано.

Алгоритм обратного дискретного преобразования Фурье отличается только тем, что вместо -j надо использовать +j и после всех вычислений поделить каждое x[k] на Nmax.

Для справки: произведение, сумма и экспонента для комплексных чисел вычисляются по формулам:

(x,y)(x',y')=(xx'-yy')(xy'+x'y)
(x,y)+(x',y')=(x+x')(y+y')
e^-jv=(cos v, - sinv)

где v - действительное число.