Вывод основных формул

Определение 1

Дана конечная последовательность x₀, x₁, x₂,...,x_N-1 (в общем случае комплексных). Дискретное преобразование Фурье (ДПФ) заключается в поиске другой последовательности X₀, X₁, X₂,...,X_N-1 элементы которой вычисляются по формуле:     (1).

Определение 2

Дана конечная последовательность X₀, X₁, X₂,...,X_N-1 (в общем случае комплексных). Обратное дискретное преобразование Фурье (ДПФ) заключается в поиске другой последовательности x₀, x₁, x₂,...,x_N-1 элементы которой вычисляются по формуле:     

Основным свойством этих преобразований (которое доказывается в соответствующих разделах математики) является тот факт, что из последовательности {x} получается (при прямом преобразовании) последовательность {X}, а если потом применить к {X} обратное преобразование, то снова получится исходная последовательность {x}.

Величина 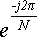постоянна и не изменяется в процессе вычисления N членов последовательности {X}. Поэтому, ее удобно вычислить один раз и обозначить как: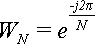

В результате формула (1) примет вид: 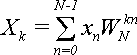  (2).

Теорема 1

Величина периодична по k и по n с периодом N. То есть, для любых целых l и m выполняется равенство:

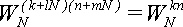    (3).

Доказательство

    (4)

Величина h = nl+mk+mlN - целая, так как все множители целые и все слагаемые целые. Далее, по формуле Эйлера, и ввиду периодичности синуса и косинуса:

e^-j2πh = cos(-2πh) + j sin(-2πh) = cos 0 + j sin 0 = 1 + j0 = 1    (5)

Подставляя (5) в (4) получаем: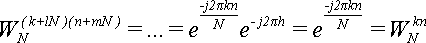

Что и требовалось доказать по (3).

Теорема 2

Для величины справедлива формула: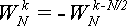

Доказательство

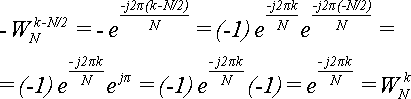
Алгоритм быстрого преобразования Фурье (БПФ) - это оптимизированный по скорости способ вычисления ДПФ. Основная идея заключается в двух пунктах.

1. Необходимо разделить сумму (1) из N слагаемых на две суммы по N/2 слагаемых, и вычислить их по отдельности. Для вычисления каждой из подсумм, надо их тоже разделить на две и т.д.
2. Необходимо повторно использовать уже вычисленные слагаемые.

Применяют либо "прореживание по времени" (когда в первую сумму попадают слагаемые с четными номерами, а во вторую - с нечетными), либо "прореживание по частоте" (когда в первую сумму попадают первые N/2 слагаемых, а во вторую - остальные). Оба варианта равноценны. В силу специфики алгоритма приходится применять только N, являющиеся степенями 2. Рассмотрим случай прореживания по времени.

Теорема 3

Определим еще две последовательности: {x_[even]} и {x_[odd]} через последовательность {x} следующим образом:

x_[even]n = x_2n,
x_[odd]n = x_2n+1,     (6)
n = 0, 1,..., N/2-1

Пусть к этим последовательностям применены ДПФ и получены результаты в виде двух новых последовательностей {X_[even]} и {X_[odd]} по N/2 элементов в каждой.

Утверждается, что элементы последовательности {X} можно выразить через элементы последовательностей {X_[even]} и {X_[odd]} по формуле: 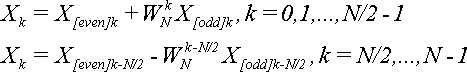(7).

Доказательство

Начинаем от формулы (2), в которую подставляем равенства из (6): 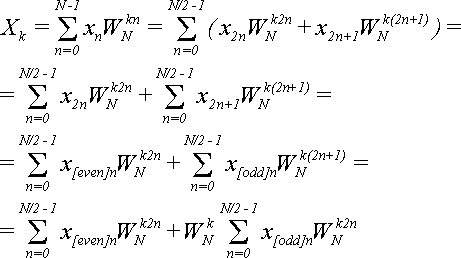    (8)

Теперь обратим внимание на то, что:

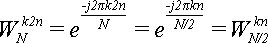    (9)

Подставляя (9) в (8) получаем:

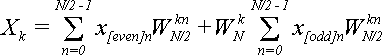  (10)

Сравним с формулами для X_[even]k и X_[odd]k при k = 0,1,…,N/2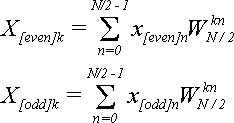-1:

    (11)

Подставляя (11) в (10) получим первую часть формулы (7):

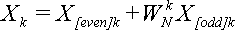
Это будет верно при k = 0,1,…,N/2-1.

Согласно теореме 1:     (12)

Подставим (12) в (10), и заменим 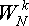по теореме 2:

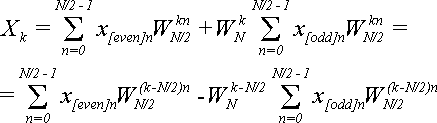    (13)

Для k = N/2,…,N-1 по формуле (2): 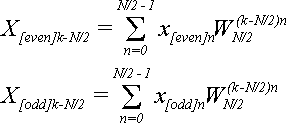    (14)

Подставляем (14) в (13):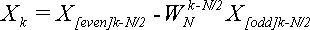

Эта формула верна для k = N/2,…,N-1 и, соответственно, (k - N/2) = 0,1,…,N/2-1 и представляет собой вторую и последнюю часть утверждения (7), которое надо было доказать.

Формула (7) позволяет сократить число умножений вдвое (не считая умножений при вычислении X_[even]k и X _[odd]k), если вычислять X_k не последовательно от 0 до N - 1, а попарно: X₀ и X_N/2, X₁ и X_N/2+1,..., X_N/2-1 и X_N. Пары образуются по принципу: X_k и X_N/2+k.

Теорема 4

ДПФ можно вычислить также по формуле: 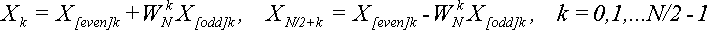    (15)

Доказательство

Согласно второй части формулы (7), получим:  

Это доказывает второе равенство в утверждении теоремы, а первое уже доказано в теореме 3.

Также по этой теореме видно, что отпадает необходимость хранить вычисленные X_[even]k и X_[odd]k после использования при вычислении очередной пары и одно вычисление 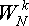можно использовать для вычисления двух элементов последовательности {X}.

На этом шаге будет выполнено N/2 умножений комплексных чисел. Если мы применим ту же схему для вычисления последовательностей {X_[even]} и {X_[odd]}, то каждая из них потребует N/4 умножений, итого еще N/2. Продолжая далее в том же духе log₂N раз, дойдем до сумм, состоящих всего из одного слагаемого, так что общее количество умножений окажется равно (N/2)log₂N, что явно лучше, чем N² умножений по формуле (2).

Рассмотрим БПФ для разных N. Для ясности добавим еще один нижний индекс, который будет указывать общее количество элементов последовательности, к которой этот элемент принадлежит. То есть X_{R}k - это k-й элемент последовательности {X_{R}} из R элементов. X_{R}[even]k - это k-й элемент последовательности {X_{R}[even]} из R элементов, вычисленный по четным элементам последовательности {X_{2R}}. X_{R}[odd]k - это k-й элемент последовательности {X_{R}[odd]}, вычисленный по нечетным элементам последовательности {X_{2R}}.

В вырожденном случае, когда слагаемое всего одно (N = 1) формула (1) упрощается до:

,

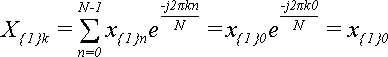Поскольку в данном случае k может быть равно только 0, то X_{1}0 = x_{1}0, то есть, ДПФ над одним числом дает это же самое число.

Для N = 2 по теореме 4 получим:

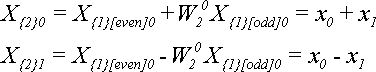
Для N = 4 по теореме 4 получим:

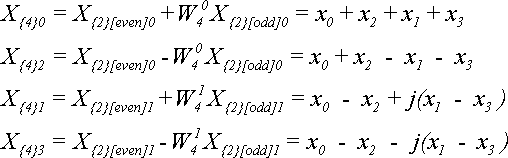
Отсюда видно, что если элементы исходной последовательности были действительными, то при увеличении N элементы ДПФ становятся комплексными.

Для N = 8 по теореме 4 получим:

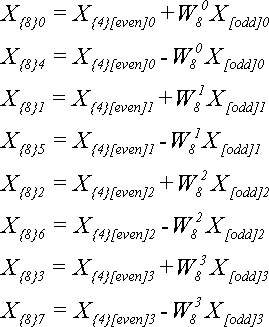
Обратите внимание, что на предыдущем шаге мы использовали степени W₄, а на этом - степени W₈. Лишних вычислений можно было бы избежать, если учесть тот факт, что

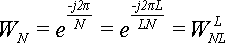
Тогда формулы для N=4 будут использовать те же W-множители, что и формулы для N=8:

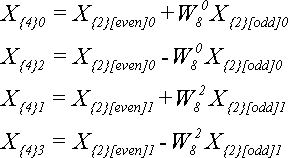
Подведем итог:

В основе алгоритма БПФ лежат следующие формулы:

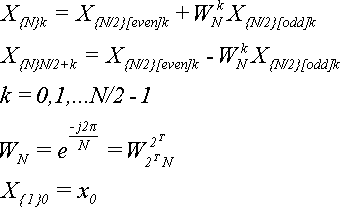    (16)